2. Matriks Negatif
Mengubah angka disetiap row dan kolom dengan mengkalikan dengan konstanta negatif.
Begitu juga jika nilai Matriks dikalikan dengan angka konstanta, misalkan jika dikalikan konstanta 2, maka hasilnya adalah semua angka yang ada di masing - masing row dan kolom dikalikan 2.
Untuk pembagian, prosesnya tidak dengan dibagi, mengkalikan dengan jalan di invers angka pembagi atau dibalikkan angka pembagi atau diberi pangkat negatif, contohnya seperti ini ;
A : B = A × B-1
3. Pengurangan
Jumlah hasil pengurangan dalam matriks, angka masing - masing di row dan kolom yang sama dikurangi, contohnya seperti di bawah ini:
Dalam penjumlahan pun sama seperti dalam pengurangan cara penyelesaiannya.
4. Transposing
Transposing atau disebut juga tukar posisi atau ubah posisi. Maka semua angka yang berada di baris row pertama berubah menjadi berada di kolom paling kanan, begitu terus berturut - turut di baris row berikutnya.
5. Notasi
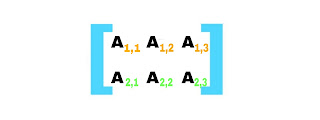
Dalam notasi, Nilai pada Matriks biasanya ditunjukkan dengan huruf kapital (seperti A, B atau C dan seterusnya). Dan setiap elemen dalam Matriks atau entri ditunjukkan oleh huruf kecil dengan posisi "subskrip" dalam baris angka dan kolom angka:
Contoh sederhana pada gambar di bawah ini ysng menunjukkan Nilai dan angka - angka elemen Matrik
A1,1 = angka di row ke-1 dan kolom ke-1 = 7
A1,2 = angka di row ke-1 dan kolom ke-2 = 8
A1,3 = angka di row ke-1 dan kolom ke-3 = 9
Dan seterusnya
Dari contoh - contoh diatas, ini mudah - mudahan dapat memberikan gambaran umum pemahaman perhitungan pada Matriks, berbagai variasi dalam kurikulum materi matriks kelas 11, matriks ordo, matriks nol, matriks baris, matriks identitas.
Matriks Matematika ini adalah basik sebagai pengenalan bahasa pemrograman dalam pembuatan berbagai aplikasi termasuk gps atau google maping, dimana bahasa pemrograman pada aplikasi didalamnya itu nerawal dari dasar - dasar dari Matriks.
Semoga bermanfaat








No comments:
Post a Comment